From Model to Screen

The Pipeline

A short rudimentary description of the pipeline might look like this:

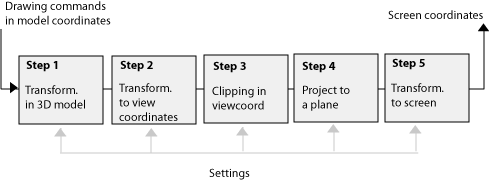
A key to understanding the process is application of the matrices in OpenGL. We choose matrix with the command:

  glMatrixMode(GL_PROJECTION);
  glMatrixMode(GL_MODELVIEW);

We know from coding that a typical setup for a projection is something like this:

  //projection matrix:
  glMatrixMode(GL_PROJECTION);
  glLoadIdentity();
  gluPerspective(...);
  // set back matrix mode: model and view
  glMatrixMode(GL_MODELVIEW);

GL_PROJECTION is the matrix used in step 4 above, while GL_MODELVIEW is the matrix used in steps 1 and 2.

We use the matrix GL_MODELVIEW when we do things like this:

  glMatrixMode(GL_MODELVIEW);
  glLoadIdentity();

  // position the eye relative to scene
  gluLookAt(...);

  // Set model in position
  glTranslatef(),
  glRotatef(...);
  ...

where both the placement of the eye, gluLookAt, and model transformations, glTranslatef and glRotatef, is part of the specifications stored in the GL_MODELVIEW-matrix.

Step 5 above, setting up the screen coordinates, is done like this:

  glViewport(...);

which tells where in the window we want to produce the projected image.

The clipping conditions, step 3, is given by specifying the viewing pyramid we want to use:

  gluPerspective(vy,aspect,front,back)

or a viewing box in stead of a pyramid

  glOrtho(xmin,xmax,ymin,ymax,front,back)

Transformations in 3D

- step 1

The modules 2D transformations and 3D transformations describes how all transformations for manipulating objects in space can be concatenated into one matrix.

Transform to View-coordinates

- step 2

The task is to describe a coordinate system with origo in the eye, and to transform the scene to this coordinate system. Different authors use slightly different terminology to describe this task. I have mainly based this explanation on the discussion given in Foley [1]. The coordinate system is described with the axis (u,v,n), and it is determined according to the following:

• View Reference Point, VRP, which is a point in a plane parallel to the projection plane.
• View Reference Normal, VRN, which is a normal to the projection plane, in VRP. VRN coincides with the n-axis in the new coordinate system.
• An eye point placed on VRN. If we have a parallel projection, we assume the eye infinitely far out on VRN.
• A description of what is up, VUP. This is necessary to identify the two last axis, u and v. The directions are given as a right-hand system, see 3D transformations

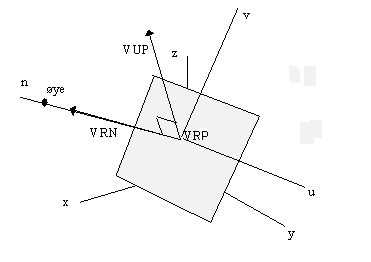
VRN-vector is vector from VRF to the eye, the viewer.

In OpenGL we can specify this coordinate system in different ways. The intuitively easiest way to to it is with:

gluLookAt(
    ex,ey,ez,  // eye
    vx,vy,vz   // looking at (VRP)
    ux,uy,uz)  // is up (VUP)

Once the new coordinate system is determined, we face the task of transforming the scene to this coordinate system, that is from the models original (x,y,z)-coordinates to the new system (u,v,n)-coordinates. This can be done by a series of transformations, translations and rotations. The problem is in principle mainly the same as doing a rotation round a any point in space. A step-by-step illustration of such a general transformation may fairly complicated, and are dropped here. See for instance Foley[1].

The advantage, once we have established this matrix, is that it may be multiplied to the general model matrix. Thus the steps 1 and 2 may be performed in one matrix operation.

OpenGL keeps this concatenated matrix as GL_MODELVIEW.

Clipping

- step 3

Both methods, glOrtho and gluPerspective defines a space that our scene should be clipped against. We have chosen not to discuss clipping in detail in this material, and will not follow up on this clipping process. It is worth noting that we can do a temporary transform to a clipping coordinate system that simplifies this algorithm.

Projection on to a plane

- step 4

Once we have got our scene into to viewing coordinate system, we can do the actual projection. To maintain a terminology according to OpenGL literature , we call the coordinates (x,y,z) in stead of (u,v,n) as we used in the reasoning above.

OpenGL keeps a matrix, GL_PROJECTION, which realize step 4.

We must decide how we want to look at the scene from the point we have chosen. There is basically two ways to do this:

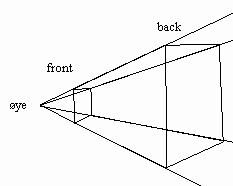
Perspective projection

  gluPerspective(vy,aspect,front,back)

vy is the angle from the viewing direction in yz-plane ,

aspect is the angle between x-axis and the vy-plane.

This specifications describes a pyramid, and is so to speak the "lens" we will look trough.

front and back cuts the pyramid with two planes parallel to the projection plane.

Parallel projection

  glOrtho(xmin,xmax,ymin,ymax,front,back)

Simply describes the box that limits what we want to include in the projection. .

Mathematics

The parallel projection is trivial. We focus on the perspective projection. We want to project the scene on to the projection plane along lines originating in the eye:

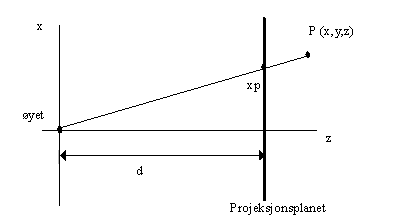
The reasoning is the same for both x- and y-axis.

We can write:

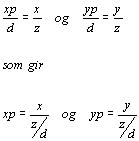
Consider the matrix:

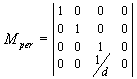
If we multiply the matrix with P, we ge:

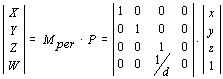
    X=x, Y=y, Z=z, W=z/d

which is not exactly what we wanted. we have however obtained a general matrix-operation, and we can fix it, by homogenisation, see Homogeneous Coordinates:

we divide with W and get:

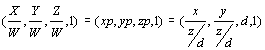
To the Screen

- step 5

All our reasoning this far has been based on an abstract 2D coordinate system. We have not considered neither extension nor resolution. When we want our scene on the screen we must relate to a finite number of points, pixels, and a fixed direction of x and y. We want a general strategy to convert any model coordinate system to the screen coordinates.

Note that traditional graphics literature operates with the term Window coordinates for model coordinates and Viewport coordinates for screen coordinates. The reason for this is that this concepts (Window and Viewport) are older than the window-on-screen technology as we know it on today's computers.

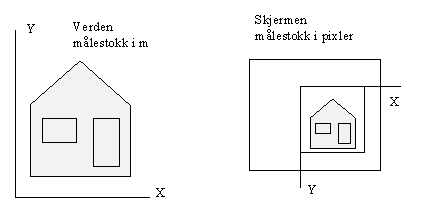
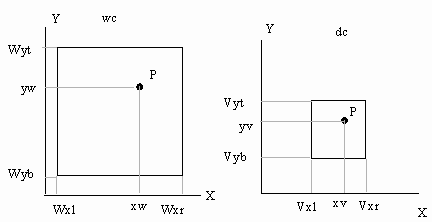
We specify a Window i wc and a Viewport i dc.

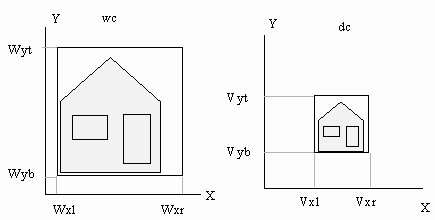
Assume Window ( Wxl,Wxr,Wyt,Wyb) and Viewport (Vxl,Vxr,Vyb,Vyt).

A mapping of point P(xw,yw) to P(xv,yv):

and

giving:

and

We can write these so we see that they introduce both a scale factor and translation:

   xv=sx(xw-Wxl)+Vxl and yv=sy(yw-Wyb)+Vyb

If we consider (xw-Wxl) and (yw-Wyb) as coordinates relative to origo in Window, we see that we can formulate this transformation as a matrix.

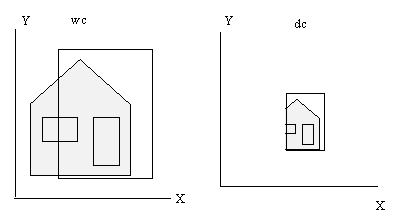
We see that the mapping from wc to dc can introduce both pan, zoom and skew

General 2D

Modern programming environments like Java and .Net has methods for operating this 2D-transformation from model to screen. We also find methods for converting screen points to model (the inverse matrix), which is very usefully when we click on screen to identify objects in a scene..

It is more ...

The description of "the pipeline" above is very rudimentary, and there are a lot of concepts in OpenGL that is not taken into account, like depth-sorting, light calculations, stencil buffers are a few.

... and then we have not even mentioned the OpenGL shading language which lets us control pixels in any detail we want.