Light and materials

When we design a GUI in an normal application or a web page and want to put color on something we give it a color by specifying a flat color. We decide that some component should be green or any combination of Red-Green-Blue (RGB). This works in normal screen design. If we want to make a fast illusion of 3d or at least some depth in the image we use some simple principles. We assume that the light source is at the screens upper left corner, and we add a light border on left and top of the component, and a dark border to the right and on bottom.

What we do is to set a color that should be emitted from the screen. We normally use a pen or a brush or some fill-command. The object is "self illuminating" and completely independent of light sources or geometry. The metaphor with pen and brush associates directly to the way we think when we draw on paper.

This model is not sufficient when we want to do 3D modeling. We must be able to administrate many light sources, take into account the geometry of the model light reflections, material properties and the position of the eye.

Type of light

...and relevant "material response"

Let us first look at different types of light.

In all calls to glLight we use the parameter lno This is to identify the light source we are addressing. An OpenGL-installation should have at least 8 possible light sources , GL_LIGHT0,GL_LIGHT1 etc.

In all calls to glMaterial we use the parameter side. side can have values GL_FRONT, GL_BACK or GL_FRONT_AND_BACK. The effect of this depends on the lighting model we choose to use, se Lighting Model below.

Ambient light

Ambient light is everywhere, it has no geometrically located source and it has no direction. Ambient light will give us a "flat" light. Geometry has no influence on how bright or dark a surface will look. It has no meaning to calculate angles since the light has no direction.

A surface will show a color that is the result of the specified ambient light and the specified material. If we have white light (1,1,1) and the material reflects only red (1,0,0), the surface will look red. We set up the an ambient light and the materials response to it this way:

   glLight(lno,GL_AMBIENT,Lar,Lag,Lab,alfa)
   glMaterial(side,GL_AMBIENT,Mar,Mag,Mab,alfa)

The alfa-value describes the translucency of the light, and side is GL_FRONT, GL_BACK or GL_FRONT_AND_BACK.

Mathematically the emitted intensity (RGB) from ambient light in a point can be expressed like this:

   Iar=Lar·Mar
   Iag=Lag·Mag
   Iab=Lab·Mab

Even if the material is determined, we can achieve some effects by changing the light. If we for instance has pure green light (0,1,0) and a surface that only reflects red (1,0,0) the surface will be black(0,0,0). If we change the light by adding some red component (0.3,1,0) the surface will turn red. If we reduce the intensity of the ambient light (0.2,0.2,0.2) the emitted light form a surface will be weaker, and the surface will look darker.

Diffuse light

Diffuse light has a direction. It may come from a defined point or may come from an infinitely remote source as parallel "light beams". This geometrical property makes it meaningful to calculate angles, and thus the lights effect on a surface will depend on the surfaces orientation.

Diffuse light is reflected equally in all directions. The illustration shows that the "light energy" that hits a surface is inversely proportional with the angle between the lights direction and the normal of the surface. That means that the energy on each surface unit decrease with the angle. This, of course, is only interesting for angles in the area <0,90> degrees.

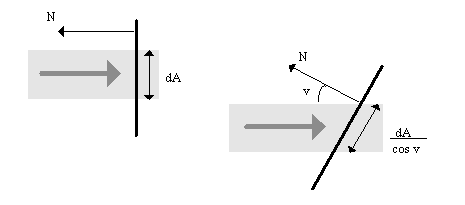
We do also have to take into account the angle between the viewing direction and the surface normal. Light reflected from a unit on the surface is proportional with the cosine of the angle between the viewing direction and the surface normal. This means that if we look directly on a surface, we should get more emitted light than if we are looking at from an angle.

The two arguments above works in opposite directions and the rule each other out. We (OpenGL) does not have to take the view direction into account when calculating the light that should be emitted from a surface.

   glLight(lno,GL_DIFFUSE,Ldr,Ldg,Ldb,alfa)
   glMaterial(side,GL_DIFFUSE,Mdr,Mdg,Mdb,alfa)

Mathematically the emitted intensity (RGB) from diffuse light in a point can be expressed like this::

   Idr=Ldr·Mdr·cos(v)
   Idg=Ldg·Mdg·cos(v)
   Idb=Ldb·Mdb·cos(v)

Where v is the angle between the surface normal and the light direction. v must be in the area <0,90> degrees.

We know that we can express cos(v) by means of the scalar product between the surface normal,N, and the light direction,L. If we assume that both are normalized (has length 1) we can write:

   Idr=Ldr·Mdr·(N·L)
   Idg=Ldg·Mdg·(N·L)
   Idb=Ldb·Mdb·(N·L)

See module Algebra

Specular light

Specular light is an attempt to model the sharp reflexes we describe as "shiny" materials. For instance white light on a red plastic ball. We get the impression that there is a white spot on the ball. reflection of shiny light is not equal in all directions.

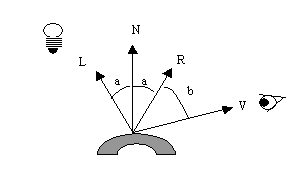
The model says that the reflected intensity is dependant of, and should be biggest for b=0. That is when the angle between the surface normal and the viewing direction is the same. There are different ways to calculate the light intensity from b. In OpenGL this is determined by the lightening model we use. see below.

There are two specifications for specular light, the component of shiny light and reflection intensity, shininess.

   glLight(lno,GL_SPECULAR,Lsr,Lsg,Lsb,alfa)
   glMaterial(side,GL_SPECULAR,Msr,Msg,Msb,alfa)
   glMaterialf(side,GL_SHININESS,sh);

We can use Phong's lightning model as basis for reasoning about this. Phong's model is based on an assumption that reflection decreases for increasing b. The relationship is expressed as: R=cosⁿ(b). Since cos < 1, increasing n will produce a sharper reflection. According to Phong we can write:

   Isr=Lsr·Msr·cossh(b)
   Isg=Lsg·Msg·cossh(b)
   Isb=Lsb·Msb·cossh(b)

Again, with normalised R and V vectors, we can write:

   Isr=Lsr·Msr·(R·V)sh
   Isg=Lsg·Msg·(R·V)sh
   Isb=Lsb·Msb·(R·V)sh

Emitted light

Emitted light is light that is emitted from the surface (material) and is the kind of light that corresponds to the color we specify when we work with normal 2D screens. If we use only emitted light in our 3D models, all angles are unimportant and the only thing that can give us a 3D impression is the form of the objects.

This light component is different from the others since it does not combine light and material properties, it depends on the material alone.

   glMaterial(side,GL_EMISSION,Mer,Meg,Meb,alfa)

The mathematics boils down to:

   Ier=Mer
   Ieg=Meg
   Ieb=Meb

Light properties

On and Off

An OpenGL implementation should have at least 8 possible sources. we can turn each of them on (enabled) and off (disabled). They are off as default:

   glEnable(GL_LIGTHn)
   glDisable(GL_LIGHTn)

where n is a number from 0 up to the number of light sources we have access to. We can also turn lightening on and off:

   glEnable(GL_LIGTHING)
   glDisable(GL_LIGTHING)

Position

A light source can have a certain position in space, or it may have a direction. The latter indicates a position infinitely far away. The position is set by:

   glLight(lno,GL_POSITION,x,y,z,w)

where w is interpreted like this: w=0 means that (x,y,z) indicates the direction of the light beams, w=1 means that (x,y,z) is the position of the light.

Default values are (0,0,-1,0), which indicates a light direction parallel to the negative z-axis.

Weakening of the light

For diffuse and specular light we have the possibility to specify that the light is weakened depending of the distance it has traveled. We may use this as an effect to help emphasize depth in a scene, or to mime effects like pollution.

We can influence the light by a factor, attenuation factor, according to this pattern:

,

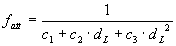where d_L is the distance to the light source and c-constants are weights. we see that not all constants can be 0. If c₁=1 and c₂=c₃=0 the light intensity is constant. These are the default values.

   glLightfv(lno,GL_CONSTANT_ATTENUATION,c)
   glLightfv(lno,GL_LINEAR_ATTENUATION,cl)
   glLightfv(lno,GL_QUADRATIC_ATTENUATION,c3)

Spotlights

We can limit the spreading of light to a cone, a spotlight effekt, to illuminate only parts of a scene. We can specify the cone and we can specify how the intensity within the cone is distributed.

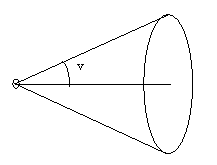
The angle between the centre of the cone and the surface can be set by glLight:

glLight(lno,GL_SPOT_CUTOFF, v),

where lno index a light source and the angle is between 0 an 90 degrees. default is downwards the negative z- axis and the spread is special value 180 degrees, which means that the light is distributed in all directions ( no spot).

Variation in intensity within the cone can be set by;

glLight(lno,GL_SPOT_EXPONENT,e)

where e is an exponent for cos to the angle between the centre in the cone and the light direction. Compare this to the Phong's model for specular light above.

There are a few things to look out for when using spotlights. Se module Shades and smoothness.

Lightening model

We can manipulate a few properties in OpenGl that influence how lights are calculated:

glLightModelfv(...)

There are three setting which are actual: general background lightning, which sides of a surface we want to influence, and reflections calculations.

General background lightening

We can specify a general ambient light, without specifying a certain light source.

   glLightModelfv(GL_LIGHT_MODEL_AMBIENT,Lgr,Lgg,Lgb,alfa)

Default values are (0.2,0.2,0.2,1.0), which is a weak white light. The contribution to the intensity from this light depends on the materials response to ambient light.

   Ier=Lgr·Mar
   Ieg=Lgg·Mag
   Ieb=Lgb·Mab

Two sides of the material

If we want to have separate light calculation on the two sides of a surface, we can do this:

  glLightModeli(GL_LIGHT_MODEL_TWO_SIDE,1);

Reflection effect

We can decide how the reflection effect is calculated, se Phong's model for reflection above.

  glLightModeli(GL_LIGHT_MODEL_LOCAL_VIEWER);

Default the calculation of shininess is calculated as if the eye is infinitely far away and the angle that describes viewing direction is the same for all coordinates in the scene. If we turn on "local viewer", as shown above, OpenGL will calculate the angle for each point based on the actual eye position. This will generally give a better result, but it costs in calculations.

All together

OpenGL works with the four light components , emitted (Le), ambient (La), diffuse (Ld) and specular (Ls). In addition we have the general ambient light (Lg). This gives us:

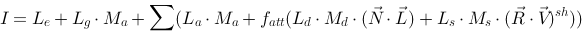
summed up for all light sources. This is the calculation that should be done for each pixel. This is not exactly what happens since OpenGL only calculate values for each vertex, and interpolates between vertices.

Vectors N, L, R and V is determined when we place objects, eye and light sources in the scene, by means of transformations. (rotate, translate, scale).

One light source

Example:

Glfloat light_ambient[]={0.0,0.0,0.0,1.0};
Glfloat light_diffuse[]={1.0,1.0,1.0,1.0};
Glfloat light_specular[]={1.0,1.0,1.0,1.0};
Glfloat light_position[]={1.0,1.0,1.0,0.0};
glLightfv(GL_LIGHT0,GL_AMBIENT,light_ambient,0);
glLightfv(GL_LIGHT0,GL_DIFFUSE,light_diffuse,0);
glLightfv(GL_LIGHT0,GL_SPECULAR,light_specular,0);
glLightfv(GL_LIGHT0,GL_POSITION,light_position,0);
glEnable(GL_LIGHING);
glEnable(GL_LIGHT0);

Note the last coordinate in the position vector. If it is 1, it means that we specify a positioned light source.

One material

Example (brass):

Glfloat mat_ambient[]={0.329412f,0.223529f,0.027451f};
Glfloat mat_diffuse[]={0.780392f,0.568627f,0.113725f };
Glfloat mat_specular[]={0.992157f, 0.941176f, 0.807843f };
glMaterialfv (GL_FRONT,GL_AMBIENT,mat_ambient,0);
glMaterialfv (GL_FRONT,GL_DIFFUSE,mat_diffuse,0);
glMaterialfv (GL_FRONT,GL_SPECULAR,mat_specularv,0);
glMaterialf (GL_FRONT,GL_SHININESS,27.89743616);

The program Material Editor described in module Material Editor may be useful to find parameters for a material.

Normals

In the light model OpenGL has to do a lot of calculations of angles. This is done by means of the dot-product of vectors. Normally we give the normal to a surface in a vertex by the glNormal-function. We can prepare the vector such that it is normalised, or we may ask OpenGL to do it for us:

glEnable(GL_NORMALIZE)

This property is default turned off, for efficiency reasons.

It is also important to be sure that normals systematically point in the "right" direction, in the sense that they point from the same side of a surface. Remember that normals are calculated as cross products according to the right hand rule. Se module Algebra. OpenGL has a function that helps us determine the direction of a surface, glFrontFace:

  glFrontFace(GL_CW)
  glFrontFace(GL_CCW)

With GL_CW we indicate that we specify points in a polygon clockwise, and GL_CCW counter clock wise. This as we observe the polygons front side.

Lightning

We can conclude that we have quite a lot of properties to work with to achieve effects. It may seems rather confusing and it is not a trivial matter to design materials and lightning of a non trivial scene. If we add the possibilities for textures, moving lights, fog and translucency, we have even more things to handle