Trampoline
We must solve three modeling problems:
- The motion of the ball
- Modeling the trampoline in a way that matches the movement of the ball
- The same with the spring
We will attempt to find some rather crude solutions that may be good enough for the purpose of visualization.
The Ball
Cosine
The basic movement we are looking for may be expressed by a parametric cosine. The expression:
z= z_start· cos(2· pi·t);
will give us what we want when we increase t by arbitrary small steps dt.
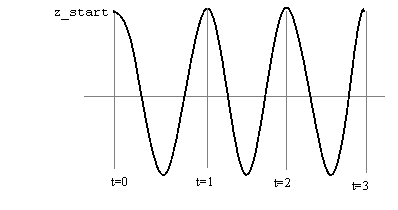
We start with t initialised to 0.
The next thing we need to do is to make sure the oscillations decrease. The ball should loose height for each period and end up in a partially stretched trampoline.
We will go for an exponential function:
f(t) = e-kt
We choose e (= 2.302585093) as basic number simply because we have a function, exp(), available for calculation. For the sake of modeling it does not matter, we can always change from one basic number to another.
The applet below gives us a possibility to experiment with the factor k in the expression:
f(t) = e-kt·cosinus(2·pi·t)
We can decide the factor k analytically. We can for instance set as a condition that the amplitude should half the starting position after three periods.
f(3) = e-3·2·pi·k = 0.5
We take the natural logarithm on both sides of the equation and and get:
k=-ln(0.5)/(3·2·pi) k=0.03 (rounded)
We leave this as a temporary and implementable description of the balls movements.
Force and mass
We choose an alternative approach based on physics. We are interested in forces acting on the ball, its acceleration, velocity and position, and reason as follows:
| k=m·a | If the ball has mass m and are subject to a force k, it will get an acceleration a. |
| dv=a·dt | The velocity of the ball, v, will change due to acceleration. It will change dv it it is accelerated in time dt. We will assume that dt is the time between each rendering of the scene. |
| dz=v·dt | The position of the ball, z, will change dz in the time span dt if the velocity is v |
There are two forces acting on the ball:
- Gravity is always there. We describe it as g·m, where m is the mass of the ball and g is the universal gravity. g is 9.81 m/s2
- The other force is the trampolines protest against being forced down. This of course depends on material and construction of the trampoline. We simplify it and assume that the force is proportional with the distance the trampoline is pressed.
We can then express the sum of the forces on the ball:
if(z>=0) sumK=m*g else sumK=m*g+m*s*z
Where z is the position of the ball and s is the resistance in the trampoline
The algorithm for the position at a certain time:
a=g;
if(z<0)
a+=s*z/m;
v+=a*dt;
v-=f*v;
z+=v*dt;
We have introduced f as a general moderation of the velocity, proportional with the velocity. We could of course formulate alternative functions for this moderation, or if we like friction.
Trampoline
The trampoline is quadratic. When in rest it coincides with the xy-plane. z-axis is pointing upwards.
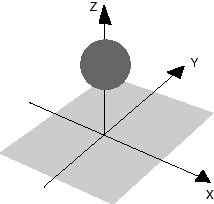
We will model the trampoline as a bezier surface, and we must decide a set of control points:
// ctrlpoints for trampoline
// 4 X 4 points, 3 coordinates each
ctrlpoints = new float[]
{
-1.5f, -1.5f, 0.0f, -0.5f, -1.5f, 0.0f,
0.5f, -1.5f, 0.0f, 1.5f, -1.5f, 0.0f,
-1.5f, -0.5f, 0.0f, -0.5f, -0.5f, 0.0f,
0.5f, -0.5f, 0.0f, 1.5f, -0.5f, 0.0f,
-1.5f, 0.5f, 0.0f, -0.5f, 0.5f, 0.0f,
0.5f, 0.5f, 0.0f, 1.5f, 0.5f, 0.0f,
-1.5f, 1.5f, 0.0f, -0.5f, 1.5f, 0.0f,
0.5f, 1.5f, 0.0f, 1.5f, 1.5f, 0.0f
};
Seen from the positive z.axis:
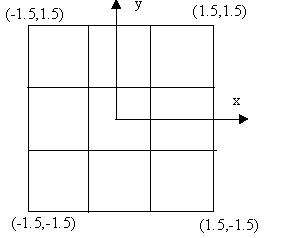
All z.values are initially 0.0. The squares on the illustration above is 0.5 x 0.5.
When the ball hits the trampoline if should yield and be pressed down. We will achieve this by moving the 4 control points in the centre downwards. The problem is to calculate how much we should move these controls points, to make the trampoline match the position of the ball.
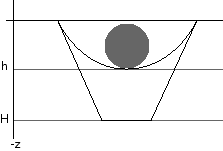
How do we set H to get a suitable h ?
We start by looking at the general formula for the Bezier surface.
![]()
and set up the following condition:
z(0.5,0.5) = h
We will leave all the points at the border of the trampoline with z-values 0. That is all control points with indices i or j equal 0 or 3. Based on symmetry we let the 4 centre points have z-value H, and we assume that the bottom position is at v=u=0.5
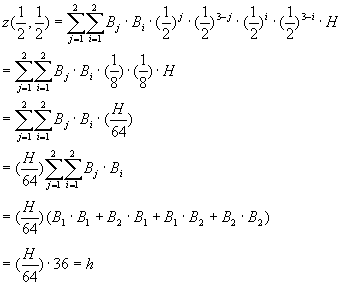
H=1.778 · h
We realize this in the following:
/////////////////////////////////////// // set nets controlpoints accordingly // adjust z-values of the 4 "center" points float h=m_SphereZ-m_SphereR; ctrlpoints[18-1]= ctrlpoints[21-1]= ctrlpoints[30-1]= ctrlpoints[33-1]=Math.min(1.778f*h,0.0f);
and
gl.glMap2f(GL.GL_MAP2_VERTEX_3,0.0f,1.0f,3,4,0.0f,1.0f,12,4,ctrlpoints,0); gl.glEnable(GL.GL_MAP2_VERTEX_3); gl.glEnable(GL.GL_AUTO_NORMAL); gl.glEnable(GL.GL_NORMALIZE); gl.glMapGrid2f(20,0.0f,1.0f,20,0.0f, 1.0f);
Spring
The Ball
The animation of a ball suspended in a spring can be modeled almost according to the same pattern as the bouncing ball. We may use the cosine/exp solution. We get a slightly different model if we use a force/mass/acceleration model.
There are two actual forces:
- Gravity works as always, described as g·m, with m as the mass of the ball and g as the universal gravity constant, 9.81 m/s2
- The other force is the springs tension when stretched. again we let this force be proportional to the length of the spring.
Forces on the ball:
sumK=m*g-m*f(z)
We use z as the balls position and f(z) as the tension of the spring. We can of course experiment with alternative f, alternative to a linear function.
The algorithm for the position of the ball at a certain point in time:
a=g-m*f(z)/m; v+=a*dt; v-=f*v; z+=v*dt;
The Spring
The spring itself is modeled as a spiral according to the following:
y(t)=r·sin(2·pi·t)
x(t)=r·cos(2·pi·t)
z(t)= k·t
Where r is the radius and k is the distance between two circles. When t runs from 0 to n, we pass n "windings" on the spring. When the spring is stretched k will increase and r will decrease.
An algorithmic description may look like this::
float topOfHelix=m_SphereZ_Start+m_SphereR+0.2f;
float incr=(topOfHelix-m_SphereZ-m_SphereR-0.2f)/circles;
// reduce radius according to stretch
float topi=(float)(2*Math.PI);
float actualR=R-incr/topi;
gl.glLineWidth(2.0f);
gl.glBegin(gl.GL_LINE_STRIP);
float t=0.0f;
float dt=0.01f;
while(t< circles)
{
gl.glVertex3f((float)(actualR*Math.cos(t*topi)),
(float)(actualR*Math.sin(t*topi)),
topOfHelix-incr*t);
t+=dt;
}
// finally to centre and down to sphere
gl.glVertex3f(0.0f,0.0f,topOfHelix-incr*t);
gl.glVertex3f(0.0f,0.0f,m_SphereZ);
gl.glEnd();
Implementation
The trampoline model and the spring suspension are implemented as two projects. They are built on the same architecture and the only thing that is different is the rendering of the model( Bezier and Spiral).
The timing is controlled by a Timer - class which kicks off a refresh of the OpenGL panel at defined intervals. Each display is modeled like this, with the two motion models as alternatives. For the spring solution:
public void display(GLAutoDrawable drawable) {
GL gl = drawable.getGL();
showScene(gl);
// do increments here,calculate spheres new position: m_SphereZ
//////////////////
// Alternative1 : acceleration version
// Experiment with stiffness and friction
accelaration=-g-stiffness*m_SphereZ/mass;
speed+=accelaration*dt;
m_SphereZ+=speed*dt;
if(speed>0)
speed-=friction*Math.abs(speed);
else
speed+=friction*Math.abs(speed);
/*
//////////////////////////////////////
// Alternative2 : cosinus version
// Experiment with numeric values on fk
aniTime+=dt;
double t=2.0f*Math.PI*aniTime;
m_SphereZ=(float)(m_SphereZ_Start*Math.exp(-fk*t)*Math.cos(t));
*/
}
For the trampoline solution
public void display(GLAutoDrawable drawable)
{
GL gl = drawable.getGL();
showScene(gl);
// do increment, calculate spheres new position: m_SphereZ
//////////////////
// Alternative1 : acceleration version
// Experiment with stiffness and friction
if(m_SphereZ>0.0f)
accelaration=-g;
else
accelaration=-g-stiffness*m_SphereZ/mass;
speed+=accelaration*dt;
m_SphereZ+=speed*dt;
if(speed>0)
speed-=friction*Math.abs(speed);
else
speed+=friction*Math.abs(speed);
/*
//////////////////////////////////////
// Alternative 2 : cosinus version
// Experiment with numeric values on fk
aniTime+=dt;
double t=2.0f*Math.PI*aniTime;
m_SphereZ=(float)(m_SphereZ_Start*Math.exp(-fk*t)*Math.cos(t));
*/
///////////////////////////////////////
// set nets controlpoints accordingly
// adjust z-values of the 4 "center" points
float h=m_SphereZ-m_SphereR;
ctrlpoints[18-1]= ctrlpoints[21-1]=
ctrlpoints[30-1]= ctrlpoints[33-1]=Math.min(1.778f*h,0.0f);
}
So What
If you analyse the modeling described above and run the two demos, there are quite a few things that may be questioned. We have been rather imprecise when it comes to the damping of the oscillations in the force/mass reasoning. We have used a linear resistance in both the trampoline and the string. You will also see that the modeling of the trampoline is not sufficiently precise when we stretch it beyond a limit ( the ball comes trough). Our simple model with 4 centre control points have some clear limitations.
The question that must be answered is however: Is it good enough for the purpose of creating an illusion of a natural" movement ? Or can we manipulate the parameters in our model to make it look "good enough" ?