Planar transformations
Translation
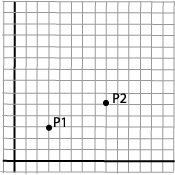 |
Translation is to move, or parallel shift, a figure. We use a simple point as a starting point. This is a simple operation that is easy to formulate mathematically. We want to move the point P1 to a new position P2.
P1=(x1,y1)=(3,3) |
We see that
x2=x1+5
y2=y1+2
This means that translation is defined by adding an offset in the x and y direction: tx and ty:
x2=x1+tx
y2=y1+ty
We assume that we can move whole figures by moving all the single points. For a many-sided figure, a polygon, this means moving all the corners.
Scaling
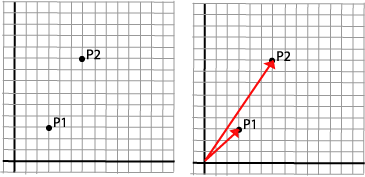
Again we will use a single point as a starting point: P1.
P1=(x1,y1)=(3,3)
We "scale" the point by multiplying it with a scaling factor in the x-direction, sx=2, and one in the y-direction, sy=3, and get
P2=(x2,y2)=(6,9)
The relation is:
x2=x1·sx
y2=y1·sy
It may seem a bit strange to say that we scale a point, since a point in a geometric sense doesn't have any area. It is better to say that we are scaling a vector.
|
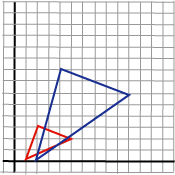
If we consider the operation on a polygon, we see that the effect becomes
a little more complicated than with translation.
In addition to moving the single points, the polygon's angles and area
is also changed.
Note: Scaling is expressed in relation to origin. |
Rotation
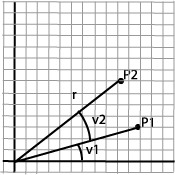 |
Rotation is more complicated to express and we have to use trigonometry to formulate it.
P1=(x1,y1)=(r·cos(v1),r·sin(v1)) |
We'll introduce the trigonometric formulas for the sum of two angles:
sin (a+b) = cos(a)·sin(b)+sin(a)·cos(b)
cos (a+b) = cos(a)·cos(b)-sin(a)·sin(b)
and get:
P1=((r·cos(v1), r·sin(v1) )
P2=(r·cos(v1)·cos(v2)-r·sin(v1)·sin(v2),
r·cos(v1)·sin(v2)+r·sin(v1)·cos(v2))
We insert:
x1=r·cos(v1)
y1=r·sin(v1)
in P2's coordinates:
P2=(x2,y2)=(x1·cos(v2)-y1·sin(v2), x1·sin(v2)+y1·cos(v2))
and we have expressed P2's coordinates with P1's coordinates and the rotation angle v.
x2= x1·cos(v)-y1·sin(v)
y2= x1·sin(v)+y1·cos(v)
Notice: Rotation is expressed relative to origin. This also means that the sides in figures that are rotated create new angles with the axes after a rotation. We assume that the positive rotation angle is counterclockwise.
Matrices
We now have the following set of equations that describes the three basic operations:
|
Translation defined by tx and ty |
x2=x1+tx |
|
Scaling defined by sx and sy |
x2=sx·x1 |
|
Rotation defined by v |
x2= x1·cos(v)-y1·sin(v) |
We want to find a common way to represent the operations. We know from linear algebra that we can represent linear dependencies like these with matrices.
If we take the equation sets directly we get:
|
Translation decided by tx and ty |
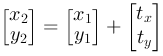
|
|
Scaling decided by sx and sy |
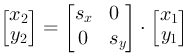
|
|
Rotation decided by v |
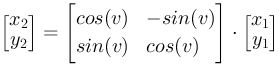
|
The matrix operations multiplication and addition are described in the module: Algebra.
Homogeneous coordinates
The three basic operations have a little different form. We want the same form and introduce homogeneous coordinates. This means that we write a position vector like this:
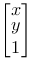
Then we can write all basic operations as multiplication between a 3 x 3 matrix and a 1 x 3 vector.
| Translation | 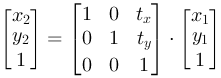
|
| Scaling | 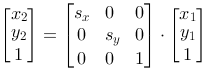
|
| Rotation | 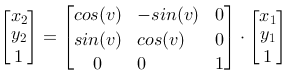
|
We have a general form
P2=M·P1
where P1 and P2 are expressed in homogeneous coordinates. We will not worry about the third coordinate, the number 1. We'll not try to give a geometric explanation of this. The whole point is to standardize the mathematics in the transformations. The third coordinate stays the same in the basic transformations and, as we will se later, in combinations of them. The module Homogeneous Coordinates discusses this subject a bit further.
Geometry
We'll use this common form of expression for many things. But first, lets look at some simple relations between matrices and geometry.
The identity matrix
An important matrix is the identity matrix:
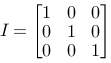
It transforms a point to itself: P1=P2=I·P1
This can be interpreted as
- translation with (0,0)
- rotation with 0 degrees, since cos (0)=1 and sin (0) =0
- scaling with (1,1)
We will need the identity matrix in many situations. In OpenGL there is a function to specify this as the current transformation matrix.
glLoadIdentity()
Later we will learn why this function is important.
Mirroring
We can mirror a point around the coordinate axes
with matrices.
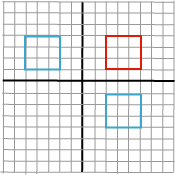
|
Around the y-axis, a scaling with (-1,0):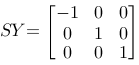 Around the x-axis, a scaling with (0,-1): 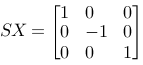
|
Shearing
A special operation called shearing is a scaling along one of the axes that depends
on the coordinate on the other axis, for example the x-axis depends on y:
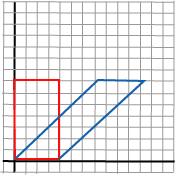
|
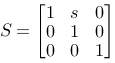
This is a representation of x2=x1+s·y
and y2=y1. The figure shows shearing used on a
rectangle and with s=1. |
Projection
We can project a point, for example onto the x-axis
with the matrix.
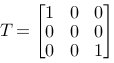
In the plane we see that the only effect from this parallel projection, is that it removes the y-coordinate. The consequence of this will always be a line along the x-axis. In space projections are more interesting.
Compound operations
It is nice to have a common form for the basic transformations. We get the profit when we see how we can combine geometric operations by combining matrices.
We can combine several geometric operations by multiplying the respective matrices. Before we do this, we can have a look at the advantages. They are essentially three:
- Rendering speed. Typically we will be in a situation where we have to calculate coordinates for a large number of points, maybe thousands, when we represent our drawing on the screen. The coordinates for these points are changed by various reasons, and their position could be the result of a large number of geometric transformations. We want to decrease the number of calculations for every point. Instead of multiplying every vector (point) with all of the matrices that are involved in turn, we want to multiply it with only one matrix. It works like this in OpenGL: There is always a current model matrix that all of the points are multiplied with.
- Modeling. We will return to this later. But let us indicate the problem for now by saying that we often have figures put together by different components. The different components are combined in a way that makes their position dependant of other parts of the figure. For example are the fingers on a robot dependant of the position of the arm they are attached to. Then it could be clever to reuse the transformations matrices several times. A practical way to do this is to have a stack of transformation matrices. This is the way it is done in OpenGL.
- We can integrate the viewing transformation with the model transformation.
Lets study some simple examples that illustrate the principle.
Two translations
We'll start with a simple example. Let us assume that we are doing two translations on a point. Let us assume that the first translation is (2,3) and that the second is (4,6). We can of course easily from geometrical considerations establish that the result should be a translation (6,9). If not, something has to be wrong with our reasoning.
The two matrices are:
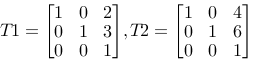
and the product:
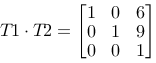
We see that the result is as desired. We achieve a matrix that realizes the compound operations by multiplying the two single matrices. We also see that in this special case we could have gotten the matrix by adding the matrices as well, but this is a special case for two translations.
We also see that in this case T1·T2=T2·T1. This is not surprising. It doesn't matter in what order the operations are done. However in general the matrix multiplication is not independent of the factor's order. This is a special case. We want to examine the relation between order and matrix multiplication closer in the next example.
Rotation around another point than origin
We consider a triangle with the corners a (1,1), b (2,-1) and c (4,2).
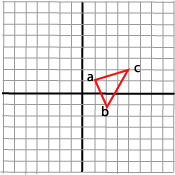
We want to rotate this triangle 90 degrees around one of its corners, a. We know that rotation, as we described it above, always is performed around origin. We have to make a strategy that combines several transformations. We try two strategies and then try to draw some conclusions.
A strategy could be:
- Move origin to rotation corner
- Rotate 90 degrees
- Move origin back
It is easy to put up the three matrices that realize the three operations.
| Move origin to the corner, a: |
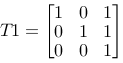
|
| Rotate 90 degrees: |
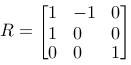
|
| Move origin back: |
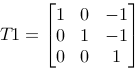
|
If we follow our reasoning we will get a matrix M=T1·R·T2, and we should get the desired effect by multiplying all the points in the triangle with this matrix, P2=M·P1.
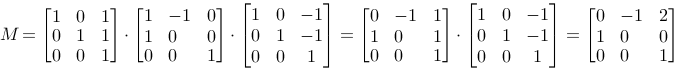
We use M on the three points in the triangle and get:
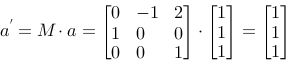
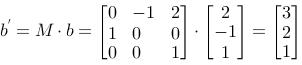
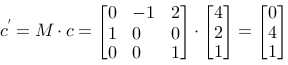
and we can draw the result:
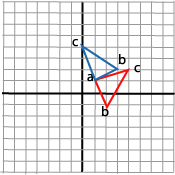
Which is what we wanted. Our strategy was successful.
An alternative strategy could be as follows:
- Move the triangle so that a ends up in origin
- Rotate 90 degrees
- Move the triangle back, so that a ends up in its original place
Since moving the point a to the origin is the opposite of moving the origin to a, the first
operation is the same as what we called T2 above. In the same way step 3, moving the triangle
back, is the same as what we called T1 above. The alternative strategy becomes: M=T2·R·T1
.
If we calculate this we get:
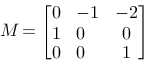
If we use this matrix on the triangle's three points we get a solution like this: which is not what we wanted.
Above we found that moving the point to origin and moving origin to the point are opposite transformations. The same transformation matrices are a part of both strategies, but the order they are used in is different. We also saw that the first strategy with moving the origin was successful. This leads to the following formulation of a strategy to couple matrices to geometric reasoning.
We can do either:
- We can go through with the reasoning on the origin, and set up the matrices in the same order as we reason.
- We can go through with the reasoning on the figure, and set up the matrices in the opposite order of the geometric reasoning.
Normally we will use strategy 1, but some times it can be easier to reason with strategy 2.
In OpenGL
To understand how OpenGL's transformations work, we have to take a closer look at the concept: current transformation matrix. It means that OpenGL always multiply coordinate values in drawing commands with the current matrix, before they are processed further and eventually, after more transformations, are rendered onto the screen. The basic drawing command in OpenGL, for plane and space respectively:
glVertex2(x,y) glVertex3(x,y,z)
The position vector which are described by the parameters is multiplied with the current transformation matrix, before it is processed further on its way to the screen. glVertex is in principle the only basic drawing primitive in OpenGL.
The most simple matrix is the identity matrix, I. It doesn't do anything with the coordinates. It is set to be the current transformation matrix with
glLoadIdentity
OpenGL has three basic functions that make up the current transformations matrix, in addition to glLoadIdentity():
glTranslate
glRotate
glScale
When we call one of these the current transformations matrix is affected by the new transformation matrix that is multiplied with it.
The example with rotation around another point than the origin, can be realized like this in OpenGL:
|
Geometric operation |
OpenGL-call | Current matrix M |
|---|---|---|
| Reset the transformations | glLoadIdentity() | M=I |
| Translate origin to a | glTranslate(1,1,0) | M =I·T1 |
| Rotate | glRotate(90,0,0,1) | M= I·T1·R |
| Translate origin back | glTranslate(-1,-1,0) | M= I·T1·R·T2 |
We see that the rotation function has parameters that both gives the rotation and the rotation axis.
The matrix stack
OpenGL offers a stack (last-in-first-out-queue) of transformation matrices, and we can push matrices to this stack and we can pop from the stack when we want to.
glPushMatrix() glPopMatrix()
This way we can keep temporary matrices (push) and get them (pop) after we have used other operations in the meantime. This strategy is very useful when drawing non-trivial figures in OpenGL (and all other graphical packages). We will return to this in program examples, but we can indicate the use with an example.
Lets look at a robot arm, with an upper arm, lower arm and three fingers:
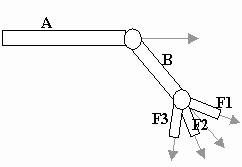 |
<draw A> glRotate() <draw B> glPushMatrix() glRotate() <draw F1> glPopMatrix() glPushMatrix() glRotate() <draw F2> glPopMatrix() glPushMatrix() glRotate() <draw F3> |
Rows and columns
In our reasoning so far we have described a point with a column vector, and we have written P2=M·P1.
As an alternative we can describe a point with a row vector and write P2=P1·M
Then we can write the three basic operations like this:
| Translation |
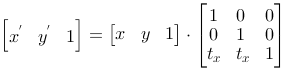 |
| Scaling |
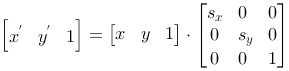 |
| Rotation |
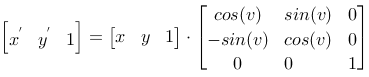 |
It can be a useful practice to calculate the consequences of this form in corresponding examples as the one we have used above. A lot of graphical literature describes transformations in this way. You can also study transposition of matrices in the module: Algebra.


