Homogeneous Coordinates

When we introduced homogeneous coordinates we did it to enable us to multiply homogeneous matrices to gain the combined geometrical effect. We found the following central 4x4 matrices in space

Identity matrix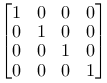	Translation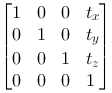	Scaling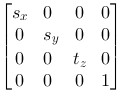
Rotation around z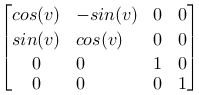	Rotation around y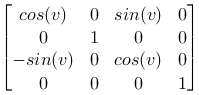	Rotation around x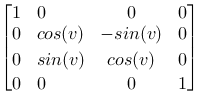

These are the matrices we normally use when we set up transformations in our models. Even though the rotation command in OpenGL is generalized and connects angle and rotation axis, the result is a combination of the matrices above.

Common for all these matrices and the matrices we get when we multiply them are that they are shaped like this:

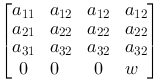
where W always have the value 1.

What happens if we make a matrix where W is different from 1?

Sometimes it's useful to calculate a matrix and use this directly, either by setting it as the current OpenGL transformations matrix or by multiplying it with the current transformation matrix. OpenGL has available commands for doing both of these operations:

glLoadMatrixd
glMultMatrixd

When OpenGL transforms a point the result is always made homogeneous. This means that the coordinate values are divided with W. Lets use a translation as an example:

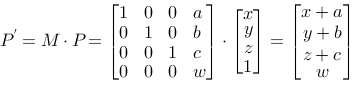
and homogeneous:

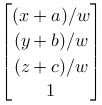
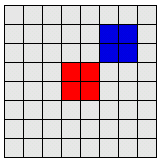The 2 code segments below produce the same figure:

drawSquare(gl,RED);
gl.glTranslatef(2.0f, 2.0f, 0.0f);
drawSquare(gl,BLUE);

drawSquare(gl,RED);
double M_mult[]={
            2,0,0,0,
            0,2,0,0,
            0,0,2,0,
            4,4,0,2
        };
gl.glMultMatrixd(M_mult,0);
drawSquare(gl,BLUE);