Shades and smoothness

Gouraud

OpenGL use a technique called Gouraud shading [1] . The basis is the calculation of the intensity of all corners of a polygon. By intensity we mean the strength of the red, green and blue component. These are as we know from the module Light and materials calculated from light components, material components and the direction of the surface. The "direction of the surface" is calculated separately for each polygon corner by giving the normal of that corner:

  glBegin(GL_TRIANGLE_STRIP);
    for(ix=0;ix< N ix++)
    {
      glNormal3f(..);
      glVertex3f(..);
    }
  glEnd();

Gouraud shading is to calculate the intensity on any point on the surface, polygon, by interpolating between the corners.

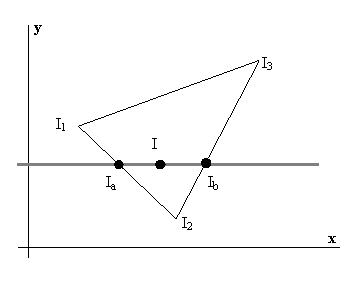
I_a is the result of interpolating between I₁ and I₂, and I_b is the result of interpolating between I₂ og I₃.

We can assume that the surface is generated line by line and that the intensity of each point is calculated according to the strategy below::

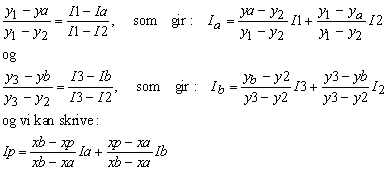
The calculations may be made more effective by investigating further the differences from one line to the next.

The two spheres below illustrates the difference between a "flat" shade and a smooth Gouraudshaded surface.

On the left sphere each surface is calculated by a constant, flat, intensity. Notice the effect caused by the eye of the observer: It looks like the borders between surfaces "stands out". This is called the Mac Band-effect and is due to the observer, not the mathematics of shading. The eye want to strengthen the borders between neighbouring surfaces.

We can turn Gouraud shading on and off in OpenGL:

  /* on */
  glShadeModel(GL_SMOOTH);
  /* off */
  glShadeModel(GL_FLAT);

Smoothing across surfaces is achieved by applying common corners as basis for intensity calculations for all surfaces that is described by the corner. For instance::

  glBegin(< mode >);
    for(ix=0;ix< N ix++)
    {
      glNormal3f(..);
      glVertex3f(..);
    }
  glEnd();

Where mode may have the following values and effects:

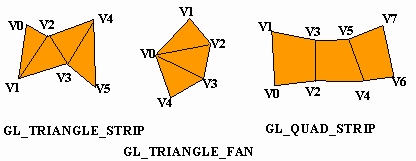
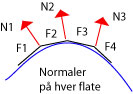
If we analyse this closer, we can see two ways to calculate and use normals. Let us assume that we want to render a smooth, "rounded", surface based on F1,F2,F3,F4.

We can calculate the normal of each surface and use the normals from surface n-1 and surface n when we render surface n. This will give an acceptable smoothing if we have small surfaces and/or small differences in directions.
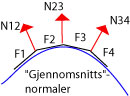
We can use normals that are the average of the normals in the border corners. This is obviously a better and more robust approach.

When we have turned on smoothing with

glShadeModel(GL_SMOOTH);

and use for instance:

  glBegin(GL_TRIANGLE_STRIP);
    for(ix=0;ix< N ix++)
    {
      glNormal3f(..);
      glVertex3f(..);
    }
  glEnd();

OpenGL will take care of the smoothing across the surfaces produces between glBegin and glEnd. Often we are in the situation where the standard polygon constructions are not sufficient to create the surface we are looking for. If we want to smooth the surface across many constructs we must take the responsibility ourselves. We can do this by using the strategy with normal averages as described above in the bordering corners.

A torus is an example where this situation appears. We can produce the torus by GL_TRIANGLE_STRIP, but we have no means of smoothing across the strips. See module Torus

To the left we have made no attempt to smooth across the triangle bands, while to the right we have made an interpolation.

Phong

An alternative to Gouraudshading is Phongshading [2] . In this case the normals are interpolated across the surface, for each point, and the intensity calculations are made based on the interpolated normals on each point on the surface. This strategy costs more but has some advantages.

Some considerations

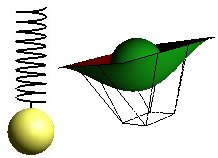
Gouraudshading has some limitations that it is important to be aware of. One consequence is that lightsources that do not "touch" a corner of a surface has no effect.

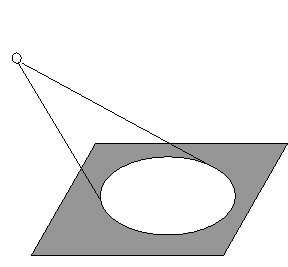
A spotlight as the one on the illustration will not give any effect on the surface since the the light do not hit a corner, and thus do not contribute to the intensity calculations in any corner.

Some effects of Gouraud shading.

From left to right:

• A sphere with flat shading (Notice the Macband effect)
• A sphere with smoothed shading
• A sphere with flat shading and a spotlight placed as headlight on the observer
• Same with smooth shading

all spheres are, in addition to the headlight, lightened from a (non spot)source up and right.

We can apply two strategies to improve the result.

• We can increase the number of surfaces
• we can model the spotlight with a softer limitation.

These effects are demonstrated below

The sphere to the left has increased number of surfaces, while the two other spheres has different degree of soft contour. The spotlight is set by

  glLighti(GL_LIGHT2, GL_SPOT_EXPONENT, m_SpotExp);

where m_SpotExp can be in the area [1,128]. Increasing number gives a smoother contour.

The Module Lamps demonstrates this.