Parametric form
Line
Let us study a straight line in a plane as a simple first example.
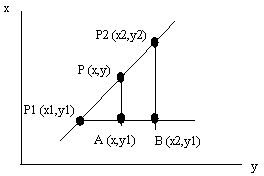
The triangles P1,A,P and P1,B,P2 are similar and we can set up the following:
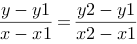
and find for example y expressed by coordinates for the two known points and x.
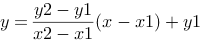
As an alternative we could set up a parametric equation for the line. Parametric means that the expression contains a parameter, t, that changes when we run along the line. For a line in the plane we get two parametric expressions, one for x and one for y. Since we have a line, both are linear.
P=P1+t·(P2-P1)
x(t)=x1+(x2-x1)·t
y(t)=y1+(y2-y1)·t
We see that x(0)=x1 and y(0)=y1, and x(1)=x2 and y(1)=y2. Since the expressions are linear we know that when t runs from 0 to 1, x and y runs from P1 to P2.
A parametric form gives control over the length of the line, not only the line direction.
Even this simple example can be useful in some situations. If we are going to carry out an animation that moves in a straight line, we can control the animation with small t-steps. We control speed by varying the t-steps. More compound movements can be controlled by a sequence of linear movements, if we don't come up with something more clever.
An extension to include lines in space is simple. If we know the end points: P1(x1,y1,z1) and P2(x2,y2,z2), we get:
P=P1+t·(P2-P1)
x(t)=x1+(x2-x1)·t
y(t)=y1+(y2-y1)·t
z(t)=z1+(z2-z1)·t
Circle
The most common way
to write a circle is:
x2 +y2 =r2.
Parametrically, this can be written as:
y(t)=r·sin(2·pi·t)
x(t)=r·cos(2·pi·t)
or if we state the angle in degrees:
y(t)=r·sin(360·t)
x(t)=r·cos(360·t)
When t runs from 0 to 1, the angle argument runs a full circle,
and the point ( x(t) , y(t) ) describes a circle.
Remember: that the trigonometric functions in C, C++ and Java expects radians as parameters, while the rotation function in OpenGL expects degrees.
Helix
A part of a helix in space, around the z-axis, can be describes as:
y(t)=r·sin(2·pi·t)
x(t)=r·cos(2·pi·t)
z(t)= k·t
Where k state the distance between two rings in the spiral. If we let t run over a larger interval, for example 0..5 we will get 5 rotations on the spiral. We also see that we have a handy mechanism to calculate circles and circle segments.
Sphere
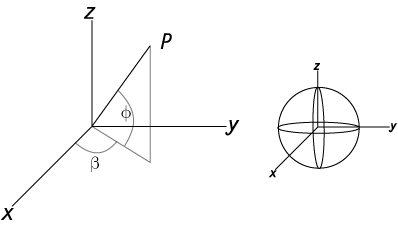
we normally describe a sphere like this, with radius r:
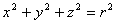
Parametrically we can describe the coordinates for a point on the spheres surface like this:
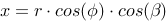
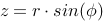
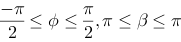
Ellipse
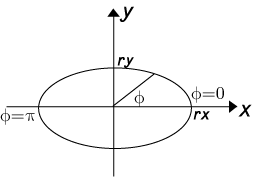
Normally we describe an ellipse like this:
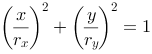
Piet Hein [1] , the Danish mathematician, poet an artist, introduced his super ellipse according to the following formula:
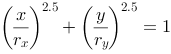
When the exponential increases, the form of the ellipse changes towards a rectangle. Piet Hein suggested that 2.5 gives us the best esthetical result. He designed Sergels torg in Stockholm as a super ellipse with the relation between the two radie 5:6.
Parametrically we describe an ellipse like this:
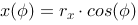
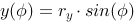
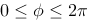
we get a super ellipse in parametric if we use an exponent n on sinus and cosinus. Note that the ellipse will grow towards a rectangle when n decreases. If rx=ry we end up with a circle, when n=1.
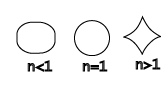
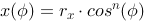
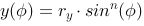
Ellipsoid
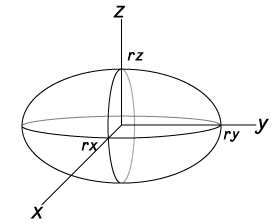
In three dimensions we describe an elliptical form like this:
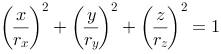
Parametrical form:
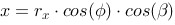
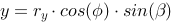
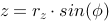
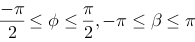
Again we get a super ellipsoid by introducing an exponent on sinus and cosinus:

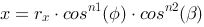
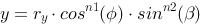
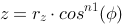
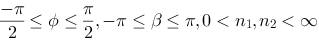
The normal in a point on the surface can be described by:
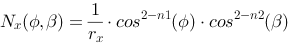
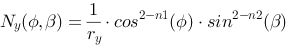
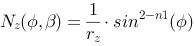
These formulas are sufficient to calculate, and thus render, a super ellipsoid. We let the two angle parameters run in a double loop and calculate neighboring points and use these to render surface fragments.
Torus

A torus is seemingly a relatively complicated mathematical figure. We want to find a parametric description of a point p on the torus's surface.
The torus is completely described by the two radii: A main radius R and the radius inside the torus' body r. We want to find two parameters that combine the two rotations that are necessary to identify a point unambiguously, one around the main axis and one around the torus body's axis.
We let w describe the rotation around the torus' main axis, "the hole", and let v describe the rotation around the torus' body. We draw the torus in two projections:
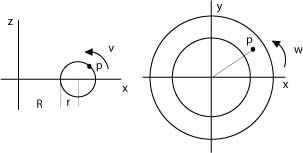
By studying the two projections we can convince ourselves that the point p's coordinates are:
z=r.sin(v) y=(R+r·cos(v))sin(w) x=(R+r·cos(v))cos(w)
This means that we can describe any point on the torus' surface with the three parametric equations above. This also enables us to limit surfaces on the torus surface with necessary precision, and we are capable of calculating normals on these surfaces (with the cross product). What remains is to find an effective algorithm to draw the torus as a mosaic of surfaces.


