Football
Geometri
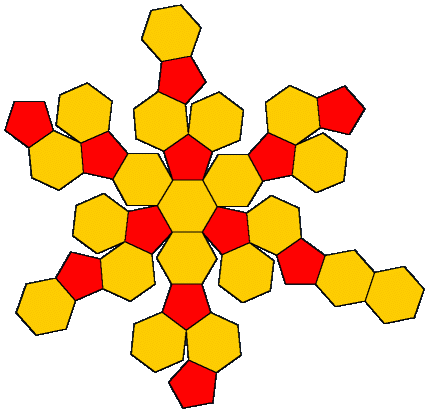
"Buckyball" is a known phenomena from mathematics [1] , nature [2] and the soccer field. The form of the buckyball is described by the golden ratio (1.61803399...). This number is calculated as the ratio between two adjacent numbers in the Fibonacci series. The number is used in many arguments in mathematics and it is found in many natural forms in nature [3] . The number often appears as a key number when forms are packed or compressed. It is also used in aesthetics as a "natural" or well-balanced ratio, for instance between the length and height of a rectangle.
Buckyball is a well known concept for chemists. It describes the position of 60 carbon atoms in the corners of the figure, as in the applet. The figure has its name from R. Buckminster Fuller [4] .
A buckyball has 60 corners, 20 polygons with 6 corners (hexagons) and 12 polygons with 5 corners (pentagons). The illustration is from GoldenNumber.net [5]
The data that is used to draw a buckyball in this module is:
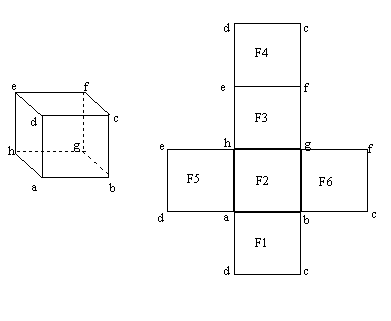
When we draw a figure based on surfaces described by a set of polygons, we will have to calculate normals and we will have to determine what is in (back) and what is out(front). We must index the corners in a consistent way. In OpenGL context this means that we must describe the corners clockwise (GL_CW) or counterclockwise(GL_CW). The direction has only meaning when we decide a point of observation. One way to do this is to decide that we look at a polygon from what we decide to call the front, usually the outside.
gl.glFrontFace(GL.GL_CW) gl.glFrontFace(GL.GL_CCW)
When we hav made these decisions we can calculate normals on all polygons, (or polygon corners) by means of the cross product for vectors.
normal6=new float[20][3];
for (int ix = 0; ix < 20; ix++)
{
float ax = p6[ix][2][0] - p6[ix][0][0];
float ay = p6[ix][2][1] - p6[ix][0][1];
float az = p6[ix][2][2] - p6[ix][0][2];
float bx = p6[ix][3][0] - p6[ix][0][0];
float by = p6[ix][3][1] - p6[ix][0][1];
float bz = p6[ix][3][2] - p6[ix][0][2];
float x = ay * bz - az * by;
float y = az * bx - ax * bz;
float z = ax * by - ay * bx;
float l=(float)Math.sqrt(x*x+y*y+z*z);
normal6[ix][0]=x/l;
normal6[ix][1]=y/l;
normal6[ix][2]=z/l;
}
normal5=new float[12][3];
for (int ix = 0; ix < 12; ix++)
{
float ax = p5[ix][2][0] - p5[ix][0][0];
float ay = p5[ix][2][1] - p5[ix][0][1];
float az = p5[ix][2][2] - p5[ix][0][2];
float bx = p5[ix][3][0] - p5[ix][0][0];
float by = p5[ix][3][1] - p5[ix][0][1];
float bz = p5[ix][3][2] - p5[ix][0][2];
float x = ay * bz - az * by;
float y = az * bx - ax * bz;
float z = ax * by - ay * bx;
float l=(float)Math.sqrt(x*x+y*y+z*z);
normal5[ix][0]=x/l;
normal5[ix][1]=y/l;
normal5[ix][2]=z/l;
}
This makes the drawing straight forward:
public void drawMe(GL gl)
{
int mode = GL.GL_POLYGON;//GL.GL_LINE_STRIP;
// 20 polygons with 6 edges
stdMaterials.setMaterial(gl, stdMaterials.MAT_WARM_WHITE, GL.GL_FRONT);
for (int p = 0; p < 20; p++)
{
gl.glBegin(mode);
gl.glNormal3f(normal6[p][0], normal6[p][1], normal6[p][2]);
for (int ix = 0; ix < 6; ix++)
gl.glVertex3f(p6[p][ix][0], p6[p][ix][1], p6[p][ix][2]);
gl.glEnd();
}
// 12 polygons with 5 edges
stdMaterials.setMaterial(gl, stdMaterials.MAT_RUBY, GL.GL_FRONT);
for (int p = 0; p < 12; p++)
{
gl.glBegin(mode);
gl.glNormal3f(normal5[p][0], normal5[p][1], normal5[p][2]);
for (int ix = 0; ix < 5; ix++)
gl.glVertex3f(p5[p][ix][0], p5[p][ix][1], p5[p][ix][2]);
gl.glEnd();
}
}
Texture
We will add texture to all hexagons. We start out with a qudratic image and want to find which coordinates in the image we want to map to the hexagons corners.
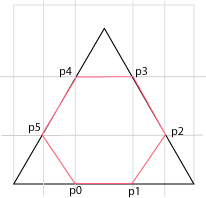
| p0 | d/3 , 0 |
| p1 | 2d/3 , 0 |
| p2 | d-(d/3)cos(60) , (d/3)sin(60) |
| p3 | d-(2d/3)cos(60) , (2d/3)sin(60) |
| p4 | (2d/3)cos(60) , (2d/3)sin(60) |
| p5 | (d/3)cos(60) , (d/3)sin(60) |
where d is the side in the triangle, and the square. When we map coordinates in a bitmap, as in the algorithm below, d always has the value 1, independant of the dimension of the bitmap measure in pixels. A texture has a logical dimension of 1 x 1.
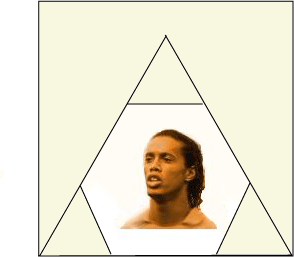
Since OpenGL (versions before 2.1) only accepts textures with format: 2n*2m,
we will compose the image such that the part we want to include fits inside the triangle in question.

Texture mapping can be prepared in the array tex6:
// calculate texture points
float d=1.0f;
float cos60=(float)Math.cos(Math.PI/3.0);//60 degrees
float sin60=(float)Math.sin(Math.PI/3.0);
tex6=new float[6][2];
tex6[0][0]=d/3.0f; tex6[0][1]=0.0f;
tex6[1][0]=2.0f*d/3.0f; tex6[1][1]=0.0f;
tex6[2][0]=d-(d/3.0f)*cos60; tex6[2][1]=(d/3.0f)*sin60;
tex6[3][0]=d-(2.0f*d/3.0f)*cos60; tex6[3][1]=(2.0f*d/3.0f)*sin60;
tex6[4][0]=(2.0f*d/3.0f)*cos60; tex6[4][1]=(2.0f*d/3.0f)*sin60;
tex6[5][0]=(d/3.0f)*cos60; tex6[5][1]=(d/3.0f)*sin60;
// load textures
textures=new TextureReader.Texture[3];
try {
textures[0] = TextureReader.readTexture("images/Marrakech.jpg");
textures[1] = TextureReader.readTexture("images/chesspiece.gif");
textures[2] = TextureReader.readTexture("images/ronaldinho.jpg");
}
catch (IOException ex) {
System.out.println(ex.getMessage());
}
Rendering:
public void drawMeTextured(GL gl,int tIx)
{
int mode = GL.GL_POLYGON;//GL.GL_LINE_STRIP;
if(tIx <0) tIx=0;
if(tIx >=textures.length) tIx=textures.length-1;
gl.glTexParameteri(GL.GL_TEXTURE_2D,GL.GL_TEXTURE_WRAP_S,GL.GL_CLAMP);
gl.glTexParameteri(GL.GL_TEXTURE_2D,GL.GL_TEXTURE_WRAP_T,GL.GL_CLAMP);
gl.glTexParameteri(GL.GL_TEXTURE_2D,GL.GL_TEXTURE_MAG_FILTER,GL.GL_NEAREST);
gl.glTexParameteri(GL.GL_TEXTURE_2D,GL.GL_TEXTURE_MIN_FILTER,GL.GL_NEAREST);
gl.glTexEnvi(GL.GL_TEXTURE_ENV,GL.GL_TEXTURE_ENV_MODE,GL.GL_MODULATE);
gl.glHint(GL.GL_PERSPECTIVE_CORRECTION_HINT,GL.GL_NICEST);
gl.glDisable(GL.GL_TEXTURE_2D);
gl.glTexImage2D(GL.GL_TEXTURE_2D, 0, GL.GL_RGB,
textures[tIx].getWidth(),textures[tIx].getHeight(), 0,
GL.GL_RGB, GL.GL_UNSIGNED_BYTE,
textures[tIx].getPixels());
gl.glEnable(GL.GL_TEXTURE_2D);
// 20 polygons with 6 edges
stdMaterials.setMaterial(gl, stdMaterials.MAT_WARM_WHITE, GL.GL_FRONT);
for (int p = 0; p < 20; p++)
{
gl.glBegin(mode);
gl.glNormal3f(normal6[p][0], normal6[p][1], normal6[p][2]);
for (int ix = 0; ix < 6; ix++)
{
gl.glTexCoord2f(tex6[ix][0], tex6[ix][1]);
gl.glVertex3f(p6[p][ix][0], p6[p][ix][1], p6[p][ix][2]);
}
gl.glEnd();
}
// 12 polygons with 5 edges
stdMaterials.setMaterial(gl, stdMaterials.MAT_RUBY, GL.GL_FRONT);
for (int p = 0; p < 12; p++)
{
gl.glBegin(mode);
gl.glNormal3f(normal5[p][0], normal5[p][1], normal5[p][2]);
for (int ix = 0; ix < 5; ix++)
gl.glVertex3f(p5[p][ix][0], p5[p][ix][1], p5[p][ix][2]);
gl.glEnd();
}
}