Linjer i planet

Vi tar utgangspunkt i problemet med å finne ut om to linjer skjærer hverandre. Dette kan angripes på mange forskjellige måter. Det er viktig å huske at for de fleste praktiske formål er vi interesserte i om to linjestykker med kjent lengde skjærer hverandre og vi er interesserte i skjæringspunktet. Dersom vi skal teste to linjestykker, må vi ta hensyn til mange ulike situasjoner. Nedenfor er tegnet noen situasjoner, der vi i tillegg til linjestykkne har tegnet ut de boksene som linjene spenner ut.

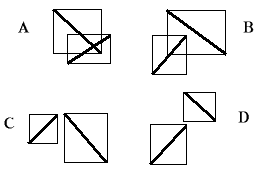
A gir oss en ekte skjæring mellom linjestykkene. B vil gi oss en "falsk" skjæring i forlengelse av det ene linjestykket, mens C vil gi oss "falsk" skjæring i forlengelse av begge linjestykkene. D er samme situasjon som B, bortsett fra at det er enklere å identifisere skjæringene som "falske" fordi de omgivende boksene ikke overlapper hverandre. C gir også adskilte bokser.

Siden det er enkelt å sjekke om bokser overlapper hverandre kan det være en fornuftig strategi å innlede testen med en bokstest. Gitt at vi har linjene p1-p2 og p3-p4.

If(min(p1.x,p2.x) > max(p3.x,p4.x)||
   min(p1.y,p2.y) > max(p3.y,p4.y)||
   min(p3.x,p4.x) > max(p1.x,p2.x)||
   min(p3.y,p4.y) > max(p1.y,p2.y) )
       < we have no intersection >

Vi har identifisert situasjoner av type C og D og sitter igjen med en situasjon av type A eller B, og vi må gå løs på selve linjebeskrivelsene. Beskrivelse av linjene fordrer divisjon og vi må ta hensyn til at linjene kan være parallelle eller parallelle med en av koordinataksene for å sikre at vi ikke dividerer med 0. Vi kan bruke følgende linjebeskrivelser:

og

og løse med hensyn på x og y. Vi ser da at vi må ta opp et spesialtilfelle dersom en av linjestykkene er parallell med y-aksen.

Det er greitt å komme fram med en slik framgangsmåte, men nedenfor er valgt en annen uttrykksform.

Vi bruker parametriske uttrykk for de to linjestykkene:

x=(p2.x-p1.x)*t + p1.x 
y=(p2.y-p1.y)*t + p1.y

x=(p4.x-p3.x)*s + p3.x 
y=(p4.y-p3.y)*s + p3.y

Parametriske uttrykk er drøftet i modulen Polynomer. Dersom vi skal finne eventuelle skjæringer mellom de to linjene kan vi løse følgende ligningssett med hensyn på s og t.

(p2.x-p1.x)*t + p1.x=(p4.x-p3.x)*s + p3.x
(p2.y-p1.y)*t + p1.y=(p4.y-p3.y)*s + p3.y

Dersom følgende betingelser er oppfylt har vi en ekte skjæring: 0<=s<=1 og 0<=t<=1.

Dette kan vi slå fast siden parametrene s og t er i området (0,1) mellom linjestykkene endepunkter.

Funksjonen nedenfor benytter parametriske ligninger for å finne en eventuell skjæring. Vi ser at vi her også må passe på en situasjon med mulig divisjon med 0. Svakheten med funksjonen er at den mellomregner med flytetall i et heltallsunivers.

BOOL Intersection(CPoint p1,CPoint p2,
                  CPoint p3,CPoint p4,
                  CPoint& ps)
{
  // finds the intersecton between lines p1-p2 and p3-p4
  // return TRUE if intersection, FALSE else
  // result in ps, if intersection
  // use parametric equations for the lines

  int dx1=p2.x-p1.x;
  int dx2=p4.x-p3.x;
  int dy1=p2.y-p1.y;
  int dy2=p4.y-p3.y;
  int n=dx2*dy1-dy2*dx1;

  if(n==0) return FALSE;
  double s=1.0*(dx1*(p3.y-p1.y)-dy1*(p3.x-p1.x))/(1.0*n);
  if ((s<0.0)||(s>1.0)) return FALSE;
  double t=1.0*(dx2*(p3.y-p1.y)-dy2*(p3.x-p1.x))/(1.0*n);
  if((t<0.0)||(t>1.0)) return FALSE;

  ps.x=(int)(dx1*t+p1.x);
  ps.y=(int)(dy1*t+p1.y);
  return TRUE;
}