Grafikk
Børre Stenseth
Moduler>Grafikk>Noen prinsipper

2D grafikk

Basistransformasjoner | Matriser | Geometri | Bibliotek | Eksempel 1 | Eksempel 2
Hva
Noen enkle prinsipper for 2D-linjegrafikk

Vi har to grunnleggende problemer å forholde oss til hver gang vi skal lage strektegninger på et skjermbilde:

  • Tegningen vår, datagrunnlaget, har dimensjoner som ikke er tilpasset punktoppløsningen på skjermen. Kanskje vi har tegnegrunnlaget vårt i mm, km eller GPS-koordinater, eller hva det måtte være.
  • Vår intuitive måte å tenke koordinatsystemer på er at origi er nede til venstre. Vi tenker nesten alltid i 1.kvadrant. Dataskjermer derimot har invertert y-aksen. Origo tilsvarer øvre venstre hjørne.

Vi kan løse dette problemet med alltid å konvertere dataene våre slik at de passer til et fast skjermoppsett, men det har en rekke ulemper. Kanskje flaten vi tegner på skal kunne skaleres, kanskje dataene endres dynamisk eller vi skal ha generelle tegnerutiner som skal kunne kombinere data fra flere kilder.

Det vi skal gjøre er å velge en annen strategi som går ut på at vi overlater til tegnebibliotekene å konvertere data etter behov. Alle ikke-trivielle programmeringsomgivelser har mekanismer for dette. Som oftest finner vi, som i .Net, en blanding av tradisjonelle transformasjonsmekanismer og noen "shortcuts". Vi skal se litt på de grunneleggende mekanismene.

Basistransformasjoner

Det bærende prinsippet er at (neste) alle transformasjoner kan bygges opp ved hjelp av en kombinasjon av følgende tre:

  • Translasjon (paralellforskyvning)
  • Rotasjon
  • Skalering

Translasjon

mat-trans

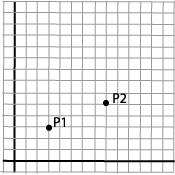Med translasjon forstår vi å flytte, eller parallellforskyve, en figur. Vi tar utgangspunkt i et enkelt punkt. Dette er en enkel operasjon som er lett å formulere matematisk. Vi vil flytte punktet P1 til en ny posisjon P2. 

	P1=(x1,y1)=(3,3)
	P2=(x2,y2)=(8,5)

Vi ser uten videre at

	x2=x1+5
	y2=y1+2

Translasjon er altså bestemt ved å addere forskyvningen i x-retningen og y-retningen: tx og ty:

	x2=x1+tx
	y2=y1+ty

Vi tar for gitt at vi kan flytte hele figurer ved å flytte alle enkeltpunktene. For en mangekant, et polygon, betyr dette å flytte alle hjørnene.

Skalering

mat-scale1

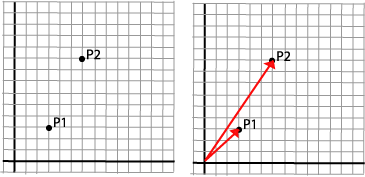
Vi tar igjen utgangspunkt i et enkelt punkt: P1.

P1=(x1,y1)=(3,3)

Vi "skalerer" punktet ved å multiplisere med en skaleringsfaktor i x-retningen, sx=2, og en i y-retningen, sy=3, og får

	P2=(x2,y2)=(6,9)

Sammenhengen er altså:

	x2=x1·sx
	y2=y1·sy

Nå virker det litt rart å si at vi skalerer et punkt, siden et punkt i geometrisk forstand er uten utstrekning. Det er bedre å si at vi skalerer en vektor.

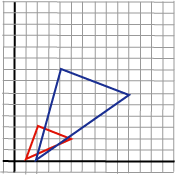
mat-scale2 Dersom vi betrakter operasjonen på et polygon, ser vi at effekten blir litt mer komplisert enn tilfellet var ved translasjon (parallellforskyvning). I tillegg til at enkeltpunktene flyttes, endres også vinkler og areal av polygonet.

Merk: Skalering er uttrykt i forhold til origo.

Rotasjon

mat-rotate

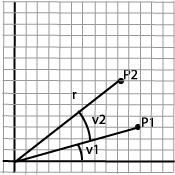Rotasjon er litt mer komplisert å uttrykke og vi må bruke trigonometri for å formulere oss.

P1=(x1,y1)=(r·cos(v1),r·sin(v1))
P2=(x2,y2)=(r·cos(v1+v2),r·sin(v1+v2))

Vi introduserer de trigonometriske formlene for summen av to vinkler:

	sin (a+b) = cos(a)·sin(b)+sin(a)·cos(b)
	cos (a+b) = cos(a)·cos(b)-sin(a)·sin(b)

og får:

	P1=((r·cos(v1), r·sin(v1) )
	P2=(r·cos(v1)·cos(v2)-r·sin(v1)·sin(v2),
	               r·cos(v1)·sin(v2)+r·sin(v1)·cos(v2))

Vi setter inn:

	x1=r·cos(v1)
	y1=r·sin(v1)

i P2s koordinater:

	P2=(x2,y2)=(x1·cos(v2)-y1·sin(v2),
	            x1·sin(v2)+y1·cos(v2))

og vi har uttrykt P2s koordinater ved hjelp av P1s koordinater og rotasjonsvinkelen v.

	x2= x1·cos(v)-y1·sin(v)
	y2= x1·sin(v)+y1·cos(v)

Merk: Rotasjon er uttrykt om origo. Det betyr også at sidene i figurer som roteres også danner nye vinkler med aksene etter rotasjonen. Vi regner positiv rotasjonsvinkel mot klokka.

Matriser

Vi sitter altså igjen med følgende ligningssett som beskriver de tre basisoperasjonene:

Translasjon
bestemt ved tx og ty		 
   x2=x1+tx
   y2=y1+ty
Skalering
bestemt ved sx og sy		 
   x2=sx·x1
   y2=sy·y1
Rotasjon
bestemt ved v		 
   x2= x1·cos(v)-y1·sin(v)
   y2= x1·sin(v)+y1·cos(v)

Vi ønsker å finne en felles form for representasjon av disse operasjonene. Vi vet fra lineær algebra at vi kan representere slike lineære sammenhenger ved matriser.

Tar vi ligningssettene direkte får vi:

Translasjon
bestemt ved tx og ty		 
|x2|   |x1|   |tx|
|  | = |  | + |  |
|y2|   |y1|   |tx|
Skalering
bestemt ved sx og sy		 
|x2|   |sx  0|   |x1|
|  | = |     | * |  |
|y2|   |0  sy|   |y1|
Rotasjon
bestemt ved v		 
|x2|   |cos(v)  -sin(v)|   |x1|
|  | = |               | * |  |
|y2|   |sin(v)   cos(v)|   |y1|

Homogene koordinater

Vi har altså litt forskjellige former for de tre basisoperasjonene. Vi ønsker samme form og introduserer homogene koordinater. Det vil si at vi skriver en posisjonsvektor slik: 

	| x |
	| y |
	| 1 |

Da kan vi skrive alle basisoperasjonene som multiplikasjon mellom en 3 x 3 matrise og en 1 x 3 vektor.

Translasjon 
| x2 |   |1 0 tx| |x1|
| y2 | = |0 1 ty|*|y1|
| 1  |   |0 0  1| |1 |
Skalering 
| x2 |   |sx 0 0| |x1|
| y2 | = |0 sy 0|*|y1|
| 1  |   |0  0 1| |1 |
Rotasjon 
| x2 |   |cos(v) -sin(v) 0| |x1|
| y2 | = |sin(v) cos(v)  0|*|y1|
| 1  |   |0        0     1| |1 |

Vi har en generell form 

      P2=M·P1

der P1 og P2 er uttrykt i homogene koordinater. Den tredje koordinaten, 1-tallet, trenger vi ikke bekymre oss. Vi forsøker ikke å gi noen geometrisk forklaring av denne. Hele vitsen med homogene koordinater er å standardisere matematikken i transformasjonene. Den tredje koordinaten forblir uforandret ved de grunnleggende transformasjonene og, som vi skal se senere, ved kombinasjoner av dem.

Geometri

Vi skal dra nytte av denne felles uttrykksformen til mange ting. La oss først se på noe enkle sammenhenger mellom matriser og geometri.

Identitetsmatrisen
En viktig matrise er identitetsmatrisen:

	  | 1 0 0 |
	I=| 0 1 0 |
	  | 0 0 1 |

Den transformerer et punkt til seg selv: P1=P2=I·P1

Dette kan vi tolke som

- translasjon med (0,0)
- rotasjon med 0 grader, siden cos (0)=1 og sin (0) =0
- skalering med (1,1)

Vi vil få bruk for identitetsmatrisen i mange situasjoner. I OpenGL er det en egen funksjon for å spesifisere denne som gjeldende transformasjonsmatrise: 

  glLoadIdentity()

Vi skal senere se hvorfor denne funksjonen er viktig.

Speiling
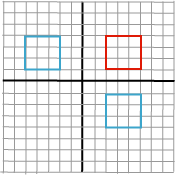
Vi kan speile et punkt om koordinataksene med matriser:

mat-mirror Om y-aksen, en skalering med (-1,0): 
	   | -1 0 0 |
	SY=| 0  1 0 |
	   | 0  0 1 |
Om x-aksen, en skalering med (0,-1): 
	   | 1 0  0 |
	SX=| 0 -1 0 |
	   | 0 0  1 |

Shearing
En spesiell operasjon som kalles shearing er en skalering langs den ene aksen som er avhengig av koordinaten på den andre aksen, f.eks. x-aksen avhengig av y:

mat-shear 
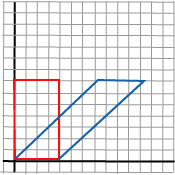
	  | 1 s 0 |
	S=| 0 1 0 |
	  | 0 0 1 |

Dette er en framstilling av x2=x1+s·y og y2=y1. Figuren viser en slik shearing anvendt på et rektangel og med s=1.
Vi ser at dette er den effekten vi finner i skråstilt, italic, skrift.

Projeksjon
Vi kan projisere et punkt, f.eks. ned på x-aksen ved matrisen 

	  | 1 0 0 |
	I=| 0 0 0 |
	  | 0 0 1 |

I planet ser vi at en slik parallellprojeksjon ikke har annen effekt enn å fjerne y-koordinaten. Konsekvensen av dette vil alltid bli en linje langs x-aksen. I rommet blir projeksjoner litt annerledes, og mer interessant.

Sammensatte operasjoner

Det er vel og bra at vi har en felles form for basistransformasjonene. Gevinsten skal vi ta ut ved å se hvordan vi kan kombinere geometriske operasjoner ved å kombinere matriser.

La oss se på noen enkle eksempler som illustrerer selve prinsippet.

To translasjoner

Vi begynner med et enkelt eksempel. La oss anta at vi skal gjennomføre to translasjoner på et punkt. La oss anta at den første translasjonen er (2,3) og at den andre er (4,6). Vi kan selvsagt lett ut fra rene geometriske betraktninger fastslå at resultatet bør være en translasjon (6,9). Hvis ikke, må det være noe galt med resonnementet vårt.

De to matrisene er altså: 

	   | 1 0 2 |        | 1 0 4 |
	T1=| 0 1 3 | og  T2=| 0 1 6 |
	   | 0 0 1 |        | 0 0 1 |

og produktet:

	      | 1 0 6 |
	T1*T2=| 0 1 9 |
	      | 0 0 1 |

Vi ser uten videre at resultatet er som ønsket. Vi oppnår en matrise som realiserer den sammensatte operasjonen ved å multiplisere de to enkeltmatrisene. Vi ser også at i dette spesielle tilfellet kunne vi få fram den samlede matrisa ved å addere de to matrisene, men det er spesielt for to translasjoner.

Vi ser også at i dette tilfellet T1·T2=T2·T1. Geometrisk er ikke dette overraskende. Det må bli det samme i hvilken rekkefølge vi utfører translasjonene. Det er imidlertid ikke slik at matrisemultiplikasjon generelt er uavhengig av faktorenes orden. Det vi har her er et spesialtilfelle. Vi vil undersøke sammenhengen mellom rekkefølge og matrisemultiplikasjon nærmere i neste eksempel.

Rotasjon om et annet punkt enn origo

Vi betrakter en trekant med hjørnene a (1,1), b (2,-1) og c (4,2).

mat-rot0

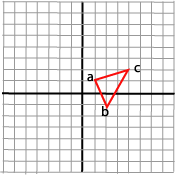
Vi ønsker å rotere denne trekanten 90 grader om sitt ene hjørne, a. Vi vet at rotasjon slik vi har beskrevet den ovenfor alltid foregår om origo. Vi må legge en strategi ved å kombinere flere transformasjoner. Vi prøver ut to strategier og forsøker å trekke noen konklusjoner etterpå.

En strategi kan være:

  1. Flytt origo til rotasjonshjørnet
  2. Roter 90 grader
  3. Flytt origo tilbake

Vi kan lett sette opp de tre matrisene som realiserer de tre enkeltoperasjonene:

Flytt origo til hjørnet a: 
   | 1 0 1 |
T1=| 0 1 1 |
   | 0 0 1 |
Roter 90 grader: 
   | 0 -1 0 |
R =| 1 0  0 |
   | 0 0  1 |
Flytt origo tilbake: 
    | 1 0 -1 |
T2 =| 0 1 -1 |
    | 0 0  1 |

Hvis vi følger resonnementet vårt vil vi få en samlematrise M=T1·R·T2, og vi skulle få den ønskede effekten ved å multiplisere alle punktene i trekanten med denne matrisa, P2=M·P1. 

    | 1 0 1 | | 0 -1 0 | | 1 0 -1 |
M = | 0 1 1 |*| 1  0 0 |*| 0 1 -1 |
    | 0 0 1 | | 0  0 1 | | 0 0  1 |

    | 0 -1 1 | | 1 0 -1 |
  = | 1 0  1 |*| 0 1 -1 |
    | 0 0  1 | | 0 0  1 |

    | 0 -1 2 |
  = | 1  0 0 |
    | 0  0 1 |

Vi anvender M på de tre punktene i trekanten og får:

         | 0 -1 2  | | 1 | | 1 |
a' = M*a | 1  0 0  |*| 1 |=| 1 |
         | 0  0 1  | | 1 | | 1 |

         | 0 -1 2  | |  2 | | 3 |
b' = M*b | 1  0 0  |*| -1 |=| 2 |
         | 0  0 1  | |  1 | | 1 |

         | 0 -1 2  | |  4 | | 0 |
c' = M*c | 1  0 0  |*|  2 |=| 4 |
         | 0  0 1  | |  1 | | 1 |

og vi kan tegne resultatet:

mat-rotrett

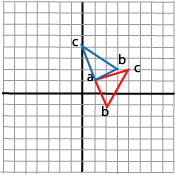
Hvilket var det vi ønsket. Strategien vår var altså vellykket.

En alternativ strategi kunne være som følger:

  1. Flytt trekanten slik at a havner i origo
  2. Roter 90 grader
  3. Flytt trekanten tilbake, slik at a havner på sitt opprinnelige

Siden det å flytte punktet a til origo er det motsatte av å flytte origo til a, så blir den førte operasjonen det samme som det vi ovenfor har kalt T2. På samme måte blir steg 3, å flytte trekanten tilbake, det samme som det vi ovenfor har kalt T1. Den alternative strategien blir da: M=T2·R·T1
. Hvis vi regner oss gjennom dette får vi: 


     | 0 -1 -2 |
 M = | 1  0  0 |
     | 0  0  1 |

Anvender vi denne matrise på trekantens tre punkter får vi en slik løsning: mat-rotfeil
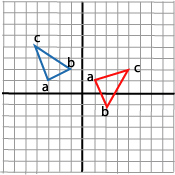
hvilket ikke overraskende er noe annet enn det vi ønsket.

Vi fant ovenfor ut at å flytte punktet til origo og å flytte origo til punktet er motsatte transformasjoner. De samme transformasjonsmatrisene inngår i begge strategiene, men rekkefølgen de anvendes på er forskjellig. Vi så videre at den første strategien med å flytte origo var vellykket. Dette kan lede oss fram til følgende formulering av en strategi for å kople matriser til geometriske resonnementer.

Vi kan gjøre ett av to:

  1. Vi kan utføre resonnementet på origo og sette opp matrisene i samme rekkefølge som vi resonnerer
  2. Vi kan utføre resonnementet på figuren og sette opp matrisene i motsatt rekkefølge av det geometriske resonnementet.

Normalt vil vi bruke strategi 1, men av og til kan det være klarere å resonnere etter strategi 2.

Bibliotek

I .Net finner vi den enkle 2D-grafikken implementert i klassene System.Drawing og System.Drawing.Drawing2D. her finner vi alt vi trenger for å tegne geometriske figurer av forskjellig slag og vi finner metoder for å adminstrere matriser som beskrevet ovenfor.

... her kommer mere

Eksempel 1

screen1

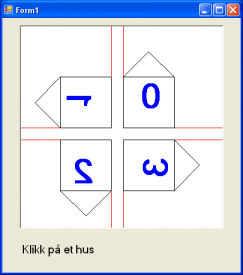
Vi bruker noen enkle transformasjoner og tegner ut en enkel figur (i fortsettelsen kalt hus) i 4 forskjellige posisjoner. Selve figuren lar seg tegne ut med følgende metode. 

private void DrawHouse(Graphics g,string name)
{
    // HW is house size
    Pen redPen = new Pen(Brushes.Red);
    Pen blackPen = new Pen(Brushes.Black);
    Font nF = new Font(this.Font.FontFamily, HW / 2, FontStyle.Bold);
     
    // draw axis
    g.DrawLine(redPen, 0, 0, 0, 2 * HW);
    g.DrawLine(redPen, 0, 0, 2 * HW, 0);
    // house
    g.DrawRectangle(blackPen, new Rectangle(0, 0, HW, HW));
    g.DrawLine(blackPen, 0, HW, HW / 2, 3 * HW / 2);
    g.DrawLine(blackPen, HW / 2, 3 * HW / 2, HW, HW);
    // draw name
    g.DrawString(name, nF, Brushes.Blue, HW / 4, HW / 4);
}
basis

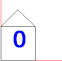
Figuren tegnes med nedre venstre hjørne i origo. Vi ønsker å tegne dette huset i fire forskjellige posisjoner, flyttet og rotert. For å få til dette bruker vi en tegnerutine som setter opp transformasjonsmatrisen for de forskjellige situasjonene. Denne tegnemetoden benytter seg som du ser av den grunnleggenede DrawHouse som er vist ovenfor: 

private void panel1_Paint(object sender, PaintEventArgs e)
{
    Graphics g = e.Graphics;
    // basic transformation to invert
    // y-axis and move to middle of panel
    g.ScaleTransform(1, -1);
    g.TranslateTransform(0, -(panel1.Height-1));
    g.TranslateTransform(2*HW, 2*HW);
    // remember this
    Matrix M = g.Transform;
    // first house
    DrawHouse(g,"0");
    
    // reset basics
    Matrix tM = M.Clone();
    tM.RotateAt(90.0f,new PointF(-10.0F,-10.0F));
    g.Transform = tM;
    DrawHouse(g,"1");
    // reset basics
    tM = M.Clone();
    tM.RotateAt(180.0f,new PointF(-10.0F,-10.0F));
    g.Transform = tM;
    DrawHouse(g, "2");
    // reset basics
    tM = M.Clone(); ;
    tM.RotateAt(270.0f, new PointF(-10.0F, -10.0F));
    g.Transform = tM;
    DrawHouse(g, "3");
}

Koden i sin helhet er slik: 

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Drawing.Drawing2D;
using System.Linq;
using System.Text;
using System.Windows.Forms;
namespace grafdemo
{
    public partial class Form1 : Form
    {
        // size of house square
        private int HW;
        public Form1()
        {
            InitializeComponent();
            HW = panel1.Height / 4;
        }
        #region paint
        private void panel1_Paint(object sender, PaintEventArgs e)
        {
            Graphics g = e.Graphics;
            // basic transformation to invert
            // y-axis and move to middle of panel
            g.ScaleTransform(1, -1);
            g.TranslateTransform(0, -(panel1.Height-1));
            g.TranslateTransform(2*HW, 2*HW);
            // remember this
            Matrix M = g.Transform;
            // first house
            DrawHouse(g,"0");
            
            // reset basics
            Matrix tM = M.Clone();
            tM.RotateAt(90.0f,new PointF(-10.0F,-10.0F));
            g.Transform = tM;
            DrawHouse(g,"1");
            // reset basics
            tM = M.Clone();
            tM.RotateAt(180.0f,new PointF(-10.0F,-10.0F));
            g.Transform = tM;
            DrawHouse(g, "2");
            // reset basics
            tM = M.Clone(); ;
            tM.RotateAt(270.0f, new PointF(-10.0F, -10.0F));
            g.Transform = tM;
            DrawHouse(g, "3");
        }
        #endregion paint
        #region drawhouse
        private void DrawHouse(Graphics g,string name)
        {
            // HW is house size
            Pen redPen = new Pen(Brushes.Red);
            Pen blackPen = new Pen(Brushes.Black);
            Font nF = new Font(this.Font.FontFamily, HW / 2, FontStyle.Bold);
             
            // draw axis
            g.DrawLine(redPen, 0, 0, 0, 2 * HW);
            g.DrawLine(redPen, 0, 0, 2 * HW, 0);
            // house
            g.DrawRectangle(blackPen, new Rectangle(0, 0, HW, HW));
            g.DrawLine(blackPen, 0, HW, HW / 2, 3 * HW / 2);
            g.DrawLine(blackPen, HW / 2, 3 * HW / 2, HW, HW);
            // draw name
            g.DrawString(name, nF, Brushes.Blue, HW / 4, HW / 4);
        }
        #endregion drawhouse
    }
}

Eksempel 2

Vi tar utgangspunkt i eksempel 1 og vil i tillegg ha mulighet for å klikke på en av "husene". Vi kan gjøre dette på mange måter. Jeg har valgt å lage en egen klasse for et hus. Denne klassen skal tegne seg og den skal kunne avgjøre om et punkt ligger inne i huset (rektangelet). Klassen er slik: 

using System;
using System.Collections.Generic;
using System.Text;
using System.Drawing;
using System.Drawing.Drawing2D;
namespace grafdemo
{
    class House
    {
        public static Font F;
        public static int HW;
        
        Matrix M;
        string HName;
        public House(string name,Matrix m)
        {
            M = m;
            HName = name;
        }
        public void DrawHouse(Graphics g)
        {
            Pen redPen = new Pen(Brushes.Red);
            Pen blackPen = new Pen(Brushes.Black);
            Font nF = new Font(F.FontFamily, HW / 2, FontStyle.Bold);
            g.Transform = M;
            // draw axis
            g.DrawLine(redPen, 0, 0, 0, 2 * HW);
            g.DrawLine(redPen, 0, 0, 2 * HW, 0);
            // house
            g.DrawRectangle(blackPen, new Rectangle(0, 0, HW, HW));
            g.DrawLine(blackPen, 0, HW, HW / 2, 3 * HW / 2);
            g.DrawLine(blackPen, HW / 2, 3 * HW / 2, HW, HW);
            // draw name
            g.DrawString(HName, nF, Brushes.Blue, HW / 4, HW / 4);
        }
        public Boolean Hit(Graphics g,int x, int y)
        {           
            // the rectangle as is in model coordinates
            Rectangle R = new Rectangle(0, 0, HW, HW);
            
            // we want to transform the hitpoint to
            // model coordinates.
            Point[] pnts=new Point[1];
            pnts[0]=new Point(x,y);
            
            Matrix IM=M.Clone();
            // since we are going the reverse way
            // (screen to model)
            IM.Invert();
            IM.TransformPoints(pnts);
            return R.Contains(pnts[0]);
       }
       public override string ToString()
       {
            return HName;
       }
    }
}

Det interessante er metoden Hit. Resonnementet er slik:

  • Vi har fått et punkt (x,y) fra et click på skjermen ( in panelet). Vi ønsker å se om dette er inne i huset
  • Vi setter opp en transformasjon som går motsatt vei av den transformasjonen som gjelder for det aktuelle huset. 
    Matrix IM=M.Clone();
IM.Invert();
  • Vi transformerer punktet. 
    IM.TransformPoints(pnts)
  • Vi sjekker om punktet er inne i huset slik det er beskrevet i modellkoordinater. 
    return R.Contains(pnts[0])

Formen er utvidet med en metode for å plukke opp museklikk i panelet og en label som sier hvor vi treffer. Det etableres en liste med hus når applikasjonen starter. 

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Drawing.Drawing2D;
using System.Text;
using System.Windows.Forms;
namespace grafdemo
{
    public partial class Form1 : Form
    {
        // size of house square
        private int HW;
        List<House> HouseList = new List<House>(4);
        public Form1()
        {
            InitializeComponent();
            MakeHouses();
        }
        #region setup
        private void MakeHouses()
        {
            // a reasonable housesize
            HW = panel1.Height / 4;
            
            // set statics (for all houses)
            House.F = panel1.Font;
            House.HW = HW;
            Graphics g = panel1.CreateGraphics();
            
            g.ScaleTransform(1, -1);
            g.TranslateTransform(0, -(panel1.Height - 1));
            g.TranslateTransform(2 * HW, 2 * HW);
            Matrix M = g.Transform;
            HouseList.Add(new House("0", M));
            
            Matrix tM = M.Clone();
            tM.RotateAt(90.0f, new PointF(-10.0F, -10.0F));
            HouseList.Add(new House("1",tM));
            tM = M.Clone();
            tM.RotateAt(180.0f, new PointF(-10.0F, -10.0F));
            HouseList.Add(new House("2",tM));
            tM = M.Clone(); ;
            tM.RotateAt(270.0f, new PointF(-10.0F, -10.0F));
            HouseList.Add(new House("3",tM));
        }
        #endregion setup
        #region paint
        private void panel1_Paint(object sender, PaintEventArgs e)
        {
            foreach (House h in HouseList)
            {
                h.DrawHouse(e.Graphics);
            }
        }
        #endregion paint
        private void panel1_MouseClick(object sender, MouseEventArgs e)
        {
            // we have hit the panel
            // have we hit any house ?
            label1.Text="";
            Graphics g = panel1.CreateGraphics();
            foreach (House h in HouseList)
            {
                if (h.Hit(g,e.X, e.Y))
                {
                    label1.Text = "Traff hus: " + h.ToString();
                    return;
                }
                label1.Text = "Traff ikke noe hus";
            }
        }
    }
}
Referanser

Eksemplene

  • Eksempel1:
    https://svn.hiof.no/svn/psource/Csharpspikes/grafdemo
  • Eksempel2:
    https://svn.hiof.no/svn/psource/Csharpspikes/grafdemo2
Vedlikehold

April 2008, B Stenseth

(Velkommen) Moduler>Grafikk>Noen prinsipper (Sjakkbrett)
HTML5
name=borres&lang=no&color=#F7F7F7
name=borres&lang=no&color=#F7F7F7